Let's assume that the temperature distribution inside a pipe is governed by the following one dimensional unsteady hyperbolic partial-differential-equation
Tt + u Tx = 0
Consider negligible heat diffusion and the initial velocity u is, 0.1 cm/s. The boundary conditions are described below:
T(x, 0) = 200 x; 0 ≤ x ≤ 0.5
T(x, 0) = 200 (1 – x); 0.5 ≤ x ≤ 1
T(x, 0) = 200 (1 – x); 0.5 ≤ x ≤ 1
Develop an algorithm in MATLAB to solve this problem using the second-order approximation in time and the second-order upwind approximation in space. Consider, Δx = 0.05 cm; Δt = 0.05.
The following MATLAB program develops the second order upwind method to solve the given one-dimensional unsteady hyperbolic convection equation.
%
Hyperbolic equation - Convection equation: Upwind Method
close all;
clc;
%
Input Properties from Problem
L=1.0; %
(dimension in cm)
Lmax=5.0;
alpha=0.01;
u=0.1; %
(dimension in cm/s)
Tt=10; %
Simulation Time Period
%
Mesh/Grid size
dx=0.05;
dt=0.05;
c=u*dt/dx;
% Depends on dt values
d=alpha*((dt/dx)^2.0);
%
Matrix Parameters
imax=(Lmax/dx)+1;
% Array dimension along the width
tmax=(Tt/dt);
% Array dimension along the height
ndim=imax-2;
tdim=tmax-2;
%
Total no of iterations
iteration=10000;
%
Convergence Criterion
tolerance=0.000001;
%
Array and Variables
% a
= Matrix of Coefficients A(i,j)
% b
= Right Side Vector, b(i)
% x
= Solution Vector, x(i)
%
Initial Condition
f(:,1)=0.0;
for i=1:imax-2
x(i)=(i-1)*dx;
if
x(i)<=1.0
f(i,1)=0.0;
end
if
x(i)>1.0 && x(i)<=1.5
f(i,1)=200*(x(i)-1.0);
end
if
x(i)>1.5 && x(i)<=2.0
f(i,1)=200*(L-x(i)+1.0);
end
if
x(i)>2.0
f(i,1)=0;
end
end
fprintf('imax =
%f\n',imax);
fprintf('c=%f\n',c);
% Upwind
Method
for t=1:tmax
time(t+1)=(t)*dt;
for
i=2:imax-2
% Second Order Approximation
f(i,t+1)=f(i,t)-c*(f(i,t)-f(i-1,t))-0.5*c*(1.0-c)*(f(i,t)-2.0*f(i-1,t)+f(i-2,t));
end
end
hold on
plot(x,f(:,1))
plot(x,f(:,find(time==1)),'o-')
plot(x,f(:,find(time==5)),'o-')
plot(x,f(:,find(time==10)),'o-')
xlabel('x, cm')
ylabel('Temperature,
C')
legend('t=0s','t=1s','t=5s','t=10s')
title ('c=0.1')
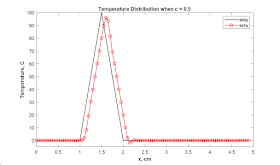
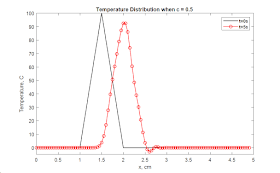
Program Output:
Second-order approximation in time and second-order upwind approximation
in space: