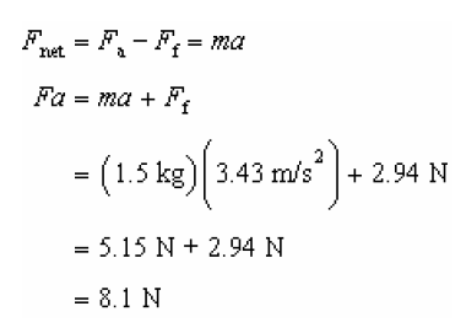In this blog post, I would like to discuss an example from the web, which may help understand better about the presence and significance of the friction force in dynamics. Friction plays a very vital role in our daily activities, for example walking, driving, etc. are all possible for us because of friction. We mostly know that the friction is a resistive force (opposes the motion), but it is also a driving force (aids the motion). The following example problem enlightens both the facts of the friction force. It is explained below.
Example Problem:
A 0.5 kg wooden block is placed on top of a 1.0 kg wooden block. The coefficient of static friction between the two blocks is 0.35. The coefficient of kinetic friction between the lower and the level table is 0.20. What is the maximum horizontal force that can be applied to the lower block without the upper block slipping?

Ff = 𝛍ₛ FN
According to the Coulomb’s friction model, this static friction is solely dependent on the weight of the body. The more the weight is the more static friction is generated. Say, if we apply a horizontal force on the lower block to move it to the right on the table as in the figure, the upper block would slide backward to the left on the table. And, this is dependent on the friction force between the block surfaces, which can resist the upper block’s sliding motion to the opposite to the lower block. For this problem, to satisfy the above mentioned condition, the friction force acting between the block surfaces must act to the right, which is acting same direction as the applied horizontal force on the lower block. This friction force will resist the upper block sliding backward and maintain the same acceleration for both of the blocks as well. Again, this friction force might be termed driving force in a sense to keep the upper block in its position while the actual driving force to create acceleration is done by the horizontal force applied on the lower block.
The following free body diagram for the upper block will show the direction of the forces and calculation of the system acceleration. Also, another free body diagram is shown later for the combined blocks where we apply the Newton’s second law to determine the required horizontal force on the lower block to keep preventing the sliding of the upper block.
From the above calculation, we see that for the upper block, the direction of acceleration and maximum friction force is the same. So, for the upper block, we may imply that the friction works as a driving force. The magnitude of the friction force is 1.7 N. Next, we are going to calculate the acceleration based on this frictional force and consider the free body diagram of the two blocks together as well.
Here, we see from the combined free body diagram of the problem that the friction force acts opposite to the applied horizontal force. The applied horizontal force to the lower block is the driving force and friction is the resistive force in this case. Now, we will calculate the net maximum horizontal force that can be applied to the lower block without the upper block slipping using the Newton’s second law of motion again.
#FreeBodyDiagram #Friction #CoulombFriction #ResistiveForce #NewtonsLaw #Blog #Blogger