This article attempts to present a general approach in designing and developing a control system for any type of electro-mechanical system. The design of any robust controller for the electro-mechanical system (for example, an airship system having payload, positioner, and antenna) should involve the following steps.
a) Identification of the governing dynamics for the system
The very first step should identify the parts/elements of the system that play meaningful roles in the overall dynamics of the system. For our airship model, there are four rigid bodies in the system: airship, payload, positioner, and antenna. They are connected in a manner to form a total dynamical system. Before moving forward with the controller, we need to figure out the appropriate dynamical equations to represent the system that needs to be controlled by a controller. To do so, we may consider the following approach.
We may attach body fixed frame to each of the rigid body of the model. The differential equation for each rigid body is derived with respect to the body fixed reference frame. We may consider the ground as an absolute or inertial frame.
Once the differential equations for the rigid bodies are done, next we do the kinematic analyses that will be used for the transformation of the differential equations from the local or body fixed frame to the global or inertial frame for analyses.
We also need to identify the forces acting on the overall system for the governing equations. In practice, there are inertial forces, gravitational forces, buoyancy forces, aerodynamic forces, and so forth that act on the airship system. We may model these forces and incorporate in the differential equations.
Based on all the above assumptions, we may end up with an 8 degree-of-freedom (DOF) system where the airship has 6 DOF, and the positioner has 2 DOF. For the controller, we need to consider these degrees of freedom as a design requirement.
b) Stability analysis of the system
We may need to linearize the system differential equations before heading towards the controller design. After the linearization, we need to check the stability of the system. Linearization may be necessary since the difficulty may arise in the controller design with complex nonlinear differential equations, which may prevent us to achieve the desired objectives. We may use the basic eigenvalue analysis to determine if the system is stable. At this stage, the linearization of the nonlinear airship model will be finalized for the design of the controller.
c) Controller design in MATLAB SIMULINK
We may choose two approaches to design a controller for the airship system. The first approach is open loop controller that is simple in design and easy to implement. The next approach may be a feedback control system that would be comprehensive and accurate in terms of system responses.
Open loop controller
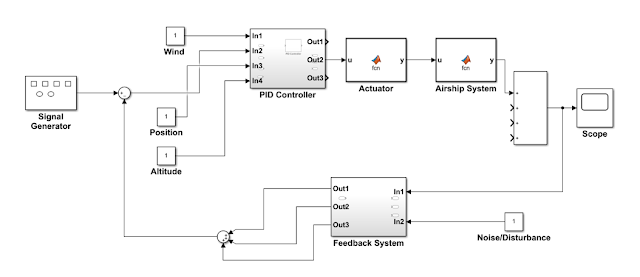
In this open loop control system design step, we may implement the following SIMULINK model, which shows an actuator block and a plant or the airship system block. We are required to control the position and altitude of the motors that are connected to the antenna and positioner, respectively.
The open loop system would be simple. The following schematic may represent the implementation method. Here, our task is to control the actuator so that it can guide the antenna. There are two actuators involved: one for 2 DOF positioner, and another for antenna. The required inputs are the desired position/altitude of the antenna that may be fed and controlled through the motor drivers. In this open loop condition, there is limited scope to optimize the system response based on the feedback errors.
Closed loop controller
We may also design a (Proportional, Integral , and Derivative) PID controller to control the position and altitude of the actuators. The following SIMULINK diagram shows a simple concept for this task:
In this closed loop feedback control system, we may design and implement a PID controller that will control the actuators for the airship model. The input to the controller may be wind disturbance, position, altitude etc. that need to taken care of precise controlling. Since the goal of this project is to position the antenna, which is also connected to a 2 DOF positioner; we may fit a PID controller in between the actuators taking considerations all the input and output parameters for the motors.
Summary
I would recommend designing the overall airship system in SolidWorks as if it represents a real physical system. Then, the computer-aided-design (CAD) model may be translated into the MATLAB environment, keeping all the physical properties same from SolidWorks. After that, in MATLAB, we may have a lot of options to design a control system conveniently, but the added benefit here is the accurate physical CAD model that needs to be controlled eventually. In SolidWorks, we may run kinematic or dynamic motion analyses to ensure the movement of each rigid part even before the development of a controller.
#ControlSystemDesign #MATLAB #SIMULINK #SolidWorks #ElectroMechanicalSystem #ModellingSimulation #FeedbackControl #MotionSimulation