As Python programming is highly hyped now-a-days and a frequent buzzword in machine learning and AI communities, I have decided to get myself familiar in this area. As I learn and decipher the Python coding day-by-day, I will be more than happy to share my coding in this blog. Here is my first program in Python - to develop a logic that adds all prime numbers between 0 and a given number.
We know that a prime number is an integer, which is greater than one and which is only divisible by one and itself. The following shows an algorithm that adds all prime numbers between 0 and a given number.
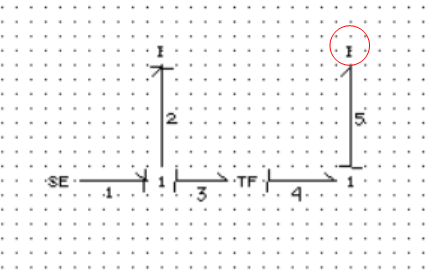
Development of an algorithm to add all prime numbers between 0 to n
I. First, we define the lower and upper number to initialize the program. For example, we set the lower number 0 and upper number 10; and we are interested to find the summation of prime numbers in this range.
II. Prime number is greater than one, so our logic begins that it must be greater than one. Therefore, we begin with number 2 and list all the numbers in our range.
III. Since, prime numbers are divisible only by itself and one; we create a loop, which confirms the prime numbers, and display them. We implement this by checking if the remainder of the number is zero or not. If the remainder is zero, then it is not a prime number.
IV. If the remainder of the number is not zero, then it is a prime number.
V. Display the prime numbers in the defined range and group the numbers in a list or array.
VI. Finally, we add all the prime numbers in the list.
The following Python code is developed based on the above algorithm, which displays all the prime numbers in a given range and add those numbers:
lower = 0
upper = 10 #Defining the range
sum1 = 0 #Setting Summation of prime numbers to zero
print("Prime numbers between", lower, "and", upper, "are:")
for num in range(lower, upper + 1):
if num > 1: #Prime number is greater than 1
for i in range(2, num):
if (num % i) == 0: #Calculates & checks remainder of division
break
else:
print(num) # Displays prime numbers
sum1 += num
print(sum1)
Program Outputs:
Prime numbers between 0 and 10 are:
2
3
5
7
17
We know that a prime number is an integer, which is greater than one and which is only divisible by one and itself. The following shows an algorithm that adds all prime numbers between 0 and a given number.
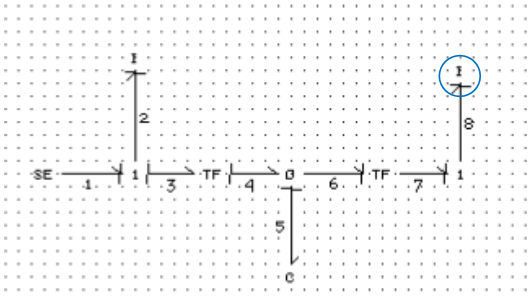
Development of an algorithm to add all prime numbers between 0 to n
I. First, we define the lower and upper number to initialize the program. For example, we set the lower number 0 and upper number 10; and we are interested to find the summation of prime numbers in this range.
II. Prime number is greater than one, so our logic begins that it must be greater than one. Therefore, we begin with number 2 and list all the numbers in our range.
III. Since, prime numbers are divisible only by itself and one; we create a loop, which confirms the prime numbers, and display them. We implement this by checking if the remainder of the number is zero or not. If the remainder is zero, then it is not a prime number.
IV. If the remainder of the number is not zero, then it is a prime number.
V. Display the prime numbers in the defined range and group the numbers in a list or array.
VI. Finally, we add all the prime numbers in the list.
The following Python code is developed based on the above algorithm, which displays all the prime numbers in a given range and add those numbers:
lower = 0
upper = 10 #Defining the range
sum1 = 0 #Setting Summation of prime numbers to zero
print("Prime numbers between", lower, "and", upper, "are:")
for num in range(lower, upper + 1):
if num > 1: #Prime number is greater than 1
for i in range(2, num):
if (num % i) == 0: #Calculates & checks remainder of division
break
else:
print(num) # Displays prime numbers
sum1 += num
print(sum1)
Program Outputs:
Prime numbers between 0 and 10 are:
2
3
5
7
17
#Blog #Blogger #Python #PrimeNumber #Algorithm