Differential equations of the system:
Notations:
m₁ = mass of the cart 1
m₂=mass of the cart 2
m₃=mass of the cart 3
m₄=mass of the cart 4
b₁=friction coefficient of cart 1
b₂=friction coefficient of cart 2
b₃=friction coefficient of cart 3
b₄=friction coefficient of cart 4
x₁=displacement of cart 1
x₂=displacement of cart 2
x₃=displacement of cart 3
x₄=displacement of cart 4
For Cart 1,
For Cart 2,
For Cart 3,
For Cart 4,
To solve the above differential equations two approaches are considered. At first the equations are simulated in SIMULINK and then validated by Bond Graph method [1].
Figure 1 represents the model of the mass-springs system. Four subsystems are used to show the differential equations of each mass. Figures 2, 3, 4 and 5 highlight the dynamic model for the cart 1, 2, 3 and 4 respectively.
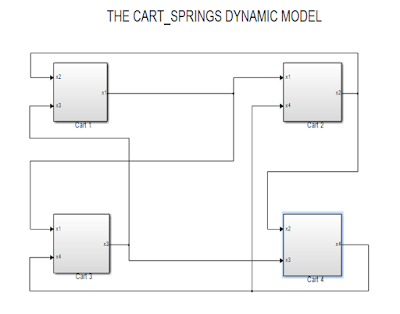
Figure 1: Showing the dynamic model of cart-springs system in SIMULINK.
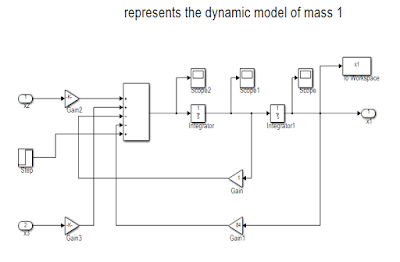
Figure 2: Showing the dynamic model of cart 1.
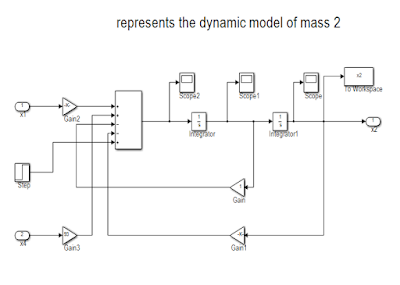
Figure 3: Showing the dynamic model of cart 2.
Figure 5: Showing the dynamic model of cart 4.
Now, the parameters given in the question are used to get the simulation results. The simulated results show the position of the each cart with respect to time. Following figures 6, 7, 8, and 9 depict the position of the cart 1, 2, 3, and 4 respectively.
Figure 6: Showing the displacement of cart 1.
Figure 7: Showing the displacement of cart 2.
Figure 8: Showing the displacement of cart 3.
Figure 9: Showing the displacement of cart 4.
As it is mentioned earlier that to validate the model another method is also taken into consideration. The system is again simulated by bond graph technique. Bond graph depicts the picture of energy flow throughout the system and it considers the states which store energy which is eventually integrally causal element in the bond graph. Inertial (-I) and compliance (-C) elements are the energy storage elements. Bond graphs “bookkeep” energy and the instantaneous energy of the system is indicated by the energy variables (p’s on –I and q’s on -C). The dissipative elements (-R) are not considered as state variable in bond graph formulation because the energy storage elements are independent if these can accept integral causality [1].
Figure 10 shows the model of the system which is developed by CAMPG [2]. The distinguishing feature of this software is the ability to generate differential equations once the model is built. Figure 11 and 12 depict the displacement of the masses which confirm the simulation results obtained by the SIMULINK.
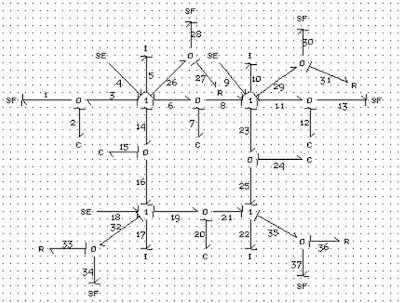
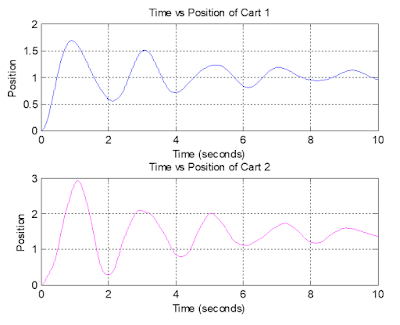
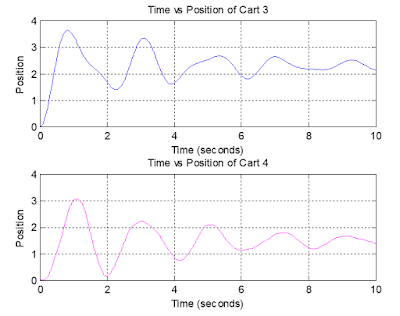
Figure 12: Showing the position of the cart 3 and 4.
Equilibrium position of the carts:
First way:
In this case, according to the question the simulation is run for longer time and the friction coefficient for each mass is changed to 100.
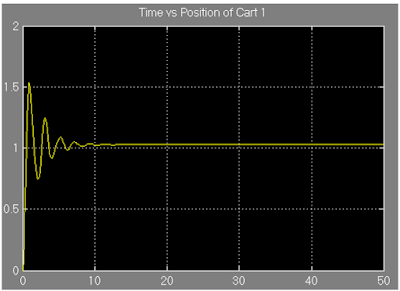
Figure 13: Showing the equilibrium position of the cart 1.
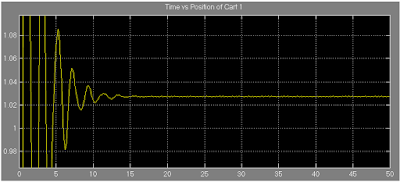
Figure 14: Showing the equilibrium position of the cart 1 (magnified).
From figure 14, the equilibrium position of the cart 1 is approximately 1.035 unit.
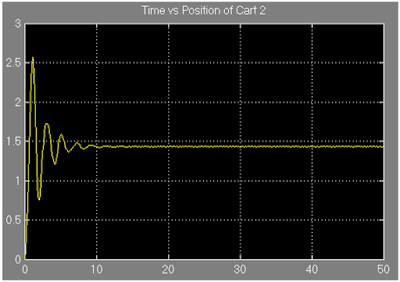
Figure 15: Showing the equilibrium position of the cart 2.
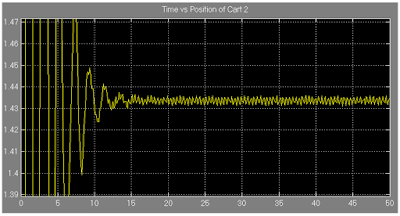
Figure 16: Showing the equilibrium position of the cart 2 (magnified).
From figure 16, it is observed that the cart 2 settles when its position is around 1.435 unit.
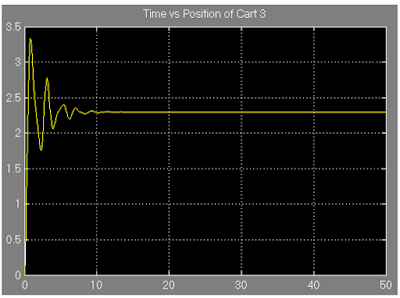
Figure 17: Showing the equilibrium position of the cart 3.
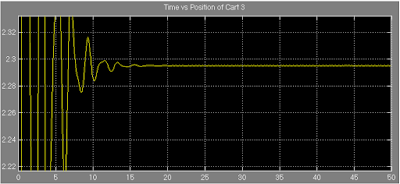
Figure 18: Showing the equilibrium position of the cart 3 (magnified).
From figure 18, it is found that the approximate equilibrium position of cart 3 is 2.29 unit.
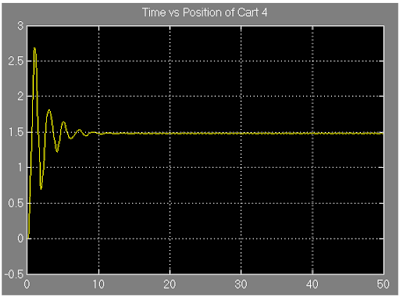
Figure 19: Showing the equilibrium position of the cart 4.
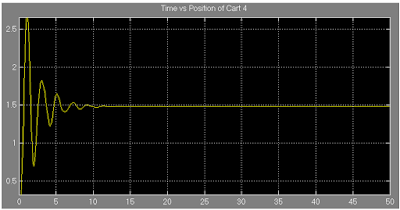
Figure 20: Showing the equilibrium position of the cart 4 (magnified).
From figure 19, the approximate equilibrium position is obtained as 1.49 unit.
The following figures 21 and 22 show the equilibrium position of cart 1,2,3, and 4 respectively which further ensure the conformity of the previous simulated results.
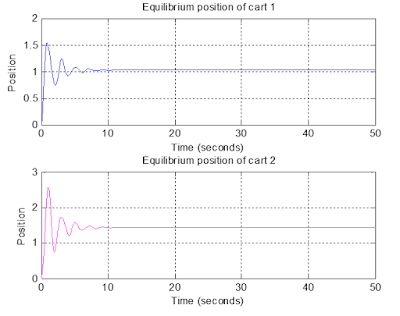
Figure 21: Showing the equilibrium position of the cart 1 and 2.
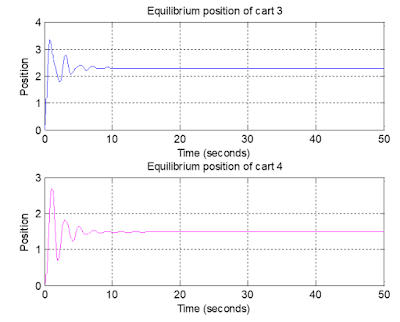
Figure 22: Showing the equilibrium position of the cart 3 and 4.
Second way:
The concept of steady state is implemented here to find out the equilibrium position of each cart. To do so, the derivative terms are considered zero. The four algebraic equations are obtained:
(1)
(2)
(3)
(4)
Substituting x1 from equation (1),
Substituting the value of x1 and x2 from equation (1) and (2) respectively,
Finally, substituting the value of x2 and x3 from equation (2) and (3) in equation (4);
x4=1.6 unit
Substituting the value of x4 in equation 3;
x3=2.34 unit
Substituting the values of x3 and x4 in equation 2;
x2=1.54 unit
Substituting the value of x2 and x3 inequation 1;
References:
[1] D. C. Karnopp, D. L. Margolis and R. C. Rosenberg, ”System Dynamics: Modeling and Simulation of Mechatronic Systems”, fourth edition, John Wiley and Sons, New Jersey, 2006.
[2] http://www.bondgraph.com/







