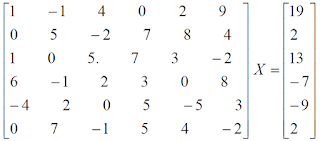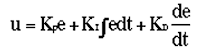A MATLAB Algorithm for a Pentadiagonal Matrix

Problem Statement: Develop a computer algorithm for the pentadiagonal matrix with band of b and solve following equations as well.

MATLAB Program to Solve a Pentadiagonal Matrix with a band b:

% A function to solve equations which coefficients have form of penta

% diagonal matrix with band b

 

function x=penta_diagonal(A,b)

 

[M,N]=size(A);

% Dimension checking

 

if M~=N

    

    error('Matrix must be square');

    

end

 

if length(b)~=M

    

    error('Matrix and vector must have the same number of rows');

    

end

 

x=zeros(N,1);

    

 

if A==A'    % Matrix symmetry checking

    

    % Band Extractions

    

    d=diag(A);

    f=diag(A,1);

    e=diag(A,2);

    

    disp(d);

    disp(f);

    disp(e);

        

    alpha=zeros(N,1);

    gamma=zeros(N-1,1);

    delta=zeros(N-2,1);

    c=zeros(N,1);

    z=zeros(N,1);

    

    % Factor A=LDL'

    

    alpha(1)=d(1);

    gamma(1)=f(1)/alpha(1);

    delta(1)=e(1)/alpha(1);

    

    alpha(2)=d(2)-f(1)*gamma(1);

    gamma(2)=(f(2)-e(1)*gamma(1))/alpha(2);

    delta(2)=e(2)/alpha(2);

    

    for k=3:N-2

        

        alpha(k)=d(k)-e(k-2)*delta(k-2)-alpha(k-1)*gamma(k-1)^2;

        gamma(k)=(f(k)-e(k-1)*gamma(k-1))/alpha(k);

        delta(k)=e(k)/alpha(k);

    end

    

    alpha(N-1)=d(N-1)-e(N-3)*delta(N-3)-alpha(N-2)*gamma(N-2)^2;

    gamma(N-1)=(f(N-1)-e(N-2)*gamma(N-2))/alpha(N-1);

    alpha(N)=d(N)-e(N-2)*delta(N-2)-alpha(N-1)*gamma(N-1)^2;

    

    % Updating Lx=b, Dc=z

    

    z(1)=b(1);

    z(2)=b(2)-gamma(1)*z(1);

    

    for k=3:N

        z(k)=b(k)-gamma(k-1)*z(k-1)-delta(k-2)*z(k-2);

    end

    

    c=z./alpha;

        

    % Back Substitution L'x=c

    

    x(N)=c(N);

    x(N-1)=c(N-1)-gamma(N-1)*x(N);

    

    for k=N-2:-1:1

        

        x(k)=c(k)-gamma(k)*x(k+1)-delta(k)*x(k+2);

    end  

   

end

 

x;

end

Program Outputs:

ans =

   0.673740053050398

  -1.021220159151194

   1.389920424403183

  -1.148541114058356

   2.055702917771884

  -2.018567639257295

A Modified Thomas Algorithm by MATLAB Codes

Modified Thomas Algorithm: For special matrices such as tridiagonal matrix, the Thomas algorithm may be applied. The given matrix in the question is not in tri-diagonal format. So, in the following program, the matrix is made tridiagonal by taking coefficients of the upper and lower triangles to the right side of the equation and then the algorithm is implemented. The initial guesses for the solutions are assumed which is corrected iteratively in the program. This means the initial guesses are substituted to the right hand side variables and then by Thomas algorithm new solutions are obtained which then again are considered as initial values based on the no of iterations and error limit. The process is simply iterative. The matrix in the following is not convergent by Thomas algorithm.

A MATLAB Program for Modified Thomas Algorithm

% Modified Thomas Algorithm to solve system of equations iteratively

 

a=[1 -1 4 0 2 9; 0 5 -2 7 8 4; 1 0 5 7 3 -2; 6 -1 2 3 0 8; -4 2 0 5 -5 3; 0 7 -1 5 4 -2]; % Given Matrix

 

b=[19; 2; 13; -7; -9; 2]; % System input

 

a1=[1 -1 0 0 0 0; 0 5 -2 0 0 0; 0 0 5 7 0 0; 0 0 2 3 0 0; 0 0 0 5 -5 3; 0 0 0 0 4 -2]; % Making original 

                                 % matrix into tridiagonal form by taking coefficients to the right side

 

c=1;

 

N=4; % No of iterations

 

e=[0.1; 0.1; 0.1; 0.1; 0.1; 0.1]; % Error tolerance

 

x(1,1)=0; x(2,1)=0; x(3,1)=0; x(4,1)=0; x(5,1)=0; x(6,1)=0; % Assuming initial solutions to continue 

                    % algorithm as the right hand side of equation contains variables with coefficient

 

 

while(c<N)

    

    x0=[x(1,1); x(2,1); x(3,1); x(4,1); x(5,1); x(6,1)];         % Initial solution

 

b1=[19-(4*x(3,1))-(2*x(5,1))-(9*x(6,1));                % Modified input matrix 

    2-(7*x(4,1))-(8*x(5,1))-(4*x(6,1));

    13-x(1,1)-(3*x(5,1))+(2*x(6,1));

    -7-(6*x(1,1))+x(2,1)-(8*x(6,1));

    -9+(4*x(1,1))-(2*x(2,1));

    2-(7*x(2,1))+x(3,1)-(5*x(4,1))];

 

%disp(b1);

 

for i=2:6           % Decomposition

    

a1(i,i-1)= a1(i,i-1)/a1(i-1,i-1);

 

a1(i,i)= a1(i,i)-(a1(i,i-1)*a1(i-1,i));

 

end

 

%a1(k,k-1)= a1(k,k-1)/a1(k-1,k-1);    

 

for i=2:6           % Forward Substitution

    

    b1(i,1) = b1(i,1)-(a1(i,i-1)*b1(i-1,1));

    

end

 

%disp(a1);

 

%disp(b1);

 

x(6,1)=b1(6,1)/a1(6,6);

 

%disp(x(6,1));

 

for i=5:-1:1        % Back Substitution

    

    x(i,1)=(b1(i,1)-(a1(i,i+1)*x(i+1,1)))/a1(i,i);

    

end

 

disp(x);

 

if ((abs(x(1:6,1))-abs(x0(1:6,1))) < e(1:6,1))  % Error checking

    

    break;

    

end

 

disp((abs(x(1:6,1))-abs(x0(1:6,1))));

 

x0=x;

 

disp(x0);

 

c=c+1;                    % loop continuation if condition is not satisfied

 

end                     % Program end

 

Program Outputs:

 

   1.0e+05 *% absolute error

   0.150253955555556

   0.087403955555556

   0.196764888888889

   0.140929777777778

   3.545057444444467

   7.086479888888927

   1.0e+05 * % solutions

  -0.150799955555556

  -0.087759955555556

  -0.197644888888889

   0.141539777777778

  -3.548047444444467

  -7.092449888888927 

A MATLAB Program to Solve a System of Non Linear Equations by Newton-Raphson Method

Problem Statement: Develop a MATLAB program to solve a system of nonlinear equations by the Newton-Raphson method, and then, test the code with the following equations:

exp(2 x₁) –x₂ -4 =0.0 
x₂ – x₃² -1 =0.0 
x₃ – sin x₁ =0.0 

Solution:
The following program is developed in MATLAB to implement the Newton-Raphson algorithm. A function named "newtonraphson" is created, which applies the technique.

% Newton-Raphson method applied to a system of non-linear equations f(x)=0,
% given the jacobian function J, where J = del(f1,f2,...,fn)/del(x1,x2,...,xn)
% and x=[x1;x2;...;xn], f=[f1;f2;...;fn]; x0 is the initial guess to run
% the program for solution

function [x,iteration] = newtonraphson(x0,f,J)

N = 100; % Maximum number of iterations definition

epsilon = 1e-15; % Tolerance Definition

maxvalue = 10000.0; % Definition of value for divergence

xxx = x0; % Initial guess for the solution

while (N>0)
   
    JJJ = feval(J,xxx);    % "feval" is used here to evaluate functions

    if abs(det(JJJ))<epsilon
        
        error('newtonraphson - Jacobian is singular - consider new x0');
        
        abort;
        
    end;
    
xn = xxx - inv(JJJ)*feval(f,xxx);  % Newton-Raphson algorithm in matrix form

    if abs(feval(f,xn))<epsilon

        x=xn;
        
        iteration = 100-N;

        return;

    end;
    
    if abs(feval(f,xxx))>maxvalue
        
        iteration = 100-N;

        disp(['iterations = ',num2str(iteration)]);
                
        error('Solution diverges');

        abort;

    end;

    N = N - 1;

    xxx = xn;

end;

error('No convergence after 100 iterations.');

abort;

end  % Function end

The following function determines the derivatives:

function [f] = funcdef(x)

% funcdef(x) = 0, with x = [x(1);x(2);x(3)] represents a system of 3 nonlinear equations

f1 = exp(2*x(1))-x(2)-4;

f2 = x(2)-(x(3)*x(3))-1;

f3 = x(3)-sin(x(1));

f = [f1;f2;f3]; % End of function



The following function determines the Jacobian:


function [J] = jacobmatrix(x)

% Evaluates the Jacobian of a 3x3 for a system of 3 nonlinear equations

J(1,1) = 2*exp(2*x(1));
J(1,2) = -1; 
J(1,3) = 0;

J(2,1) = 0; 
J(2,2) = 1; 
J(2,3) = -2*x(3);

J(3,1) = -cos(x(1)); 
J(3,2) = 0; 
J(3,3) = 1;

end  % Function end

Program Outputs:

>> [x,iteration] = newtonraphson([1;1;1],'funcdef','jacobmatrix')
x =
    0.8590
    1.5733
    0.7572
iteration =
     4

>> funcdef([0.85;1.57;0.75])
ans =
   -0.0961
    0.0075
   -0.0013

So, the solutions are 0.85, 1.57 and 0.75.

Successive over Relaxation (SOR) Method to Solve System of Equations

Problem: Develop a MATLAB code to solve the following system of algebraic equations using the Successive-over-Relaxation Method.

Solution:

Successive over Relaxation Method: This method is just the modification of the Gauss-Seidel method with an addition relaxation factor 𝛚. This method gives convergent solution as there is an option for under relaxation when 𝛚 is less than one. For different 𝛚, the following program can determine the solution. However, when 𝛚 is 0.05, the relatively better results are obtained.

MATLAB Program for Successive Over Relaxation (SOR) Method

function x = sor(a,b,x0,e,N,w)

% a - (nxn) matrix

% b - column vector of length n

% x0 - initial solution

% e - error definition

% N - no. of iterations

% w – relaxation factor

 

format long;

 

m=size(a,1); 

 

n=length(b);

 

p=length(x0);

 

q=length(e);

 

if (m ~= n)

    

    error('a and b do not have the same number of rows')

    

end

 

y0=x0;

 

for i=1:m

   

    [~,f]=max(abs(a(1:m,i:i))); 

                             

   % disp(f);  

 

    a([i,f],1:n)=a([f,i],1:n);                 

                                                                                       

end

 

for t=1:m

    

if a(t,t)==0

    

   [~,g]=max(abs(a(1:m,t:t)));            

        

   a([t,g],1:n)=a([g,t],1:n);

        

end

 

end

    

% disp(a);

 

c=1;

 

while(c<N)

 

for j=1:m  

    

    for k=1:p

        

        Z(1,k)=(a(j,1:n)*y0(1:p,1));

                                                                    

    end

    

    Y(j:j,1)=sum(Z(1,k)); 

       

   % disp(Y);

           

    R(j:j,1)=b(j:j,1)-Y(j:j,1);

    

   % disp (R);

                     

    x(j:j,1)=y0(j:j,1)+((R(j:j,1)*w)/a(j:j,j:j));

            

    y0(j:j,1)= x(j:j,1); 

    

   % disp (y0);    

   % disp (x);

               

end

 

if (abs(x(1:p,1)-x0(1:p,1)) < e(1:q,1))

    

    break;

    

end

 

disp (x);

disp(abs(x(1:p,1)-x0(1:p,1)));

    

x0=y0;

 

c=c+1;

 

end

 

x=x(1:p,1);

       

end

 

Program Outputs:

ans =

   2.322822494693882

   0.675693020694401

   2.160169880982512

  -0.350429027969758

  -0.428941223493063

  -0.394923172868219 

 

Error Percentage: 2.2%, 1.5%, 1.4%, 2.6%, 0.9% and 5.8%.

Gauss-Seidel Iteration Method to Solve System of Algebraic Equations

The following matrix represents a system of linear algebraic equations. In this problem, we are going to solve these equations by applying Gauss-Seidel iteration approach.

The following program solves system of linear algebraic equations iteratively with successive approximation by using most recent solution vectors. However, there is a condition to work for this program which is strictly diagonal dominance. And, the given matrix in question is not diagonally dominant although matrix switching operations are carried out. For this circumstance, convergence is not guaranteed and the program shows the problem while calculating error as it increases with no of iterations.

MATLAB Program for Gauss-Seidel Iterative Method

% Gauss-Seidel Iterative Algorithm

 

function x = gauss_seidal(a,b,x0,e,N) 

 

% a - (nxn) matrix

% b - column vector of length n

% x0 - initial solution

% e - error definition

% N - no. of iterations

 

format long;

 

m=size(a,1);   % get number of rows in matrix a

 

n=length(b);   % get length of b

 

p=length(x0);  % get length of x0

 

q=length(e);   % get length of e

 

if (m ~= n)

    

    error('a and b do not have the same number of rows')

    

end

 

y0=x0;

 

for i=1:m       % Interchanging row/column to make diagonally dominant matrix

   

    [~,f]=max(abs(a(1:m,i:i))); 

                             

   % disp(f);  

 

    a([i,f],1:n)=a([f,i],1:n);                 

                                                                                       

end

 

for

             % while switching rows. This loop just interchange between rows to avoid '0'

    

if a(t,t)==0

    

   [~,g]=max(abs(a(1:m,t:t)));            

        

   a([t,g],1:n)=a([g,t],1:n);

        

end

 

end

    

 disp(a);

 

c=1;

 

while(c<N)

 

for j=1:m   % Successive iteration, most recent solution used for next calculation

    

    for k=1:p

        

        Z(1,k)=(a(j,1:n)*y0(1:p,1));

                                                                    

    end

    

    Y(j:j,1)=sum(Z(1,k)); 

       

   % disp(Y);

           

    R(j:j,1)=b(j:j,1)-Y(j:j,1);

    

   % disp (R);

                     

    x(j:j,1)=y0(j:j,1)+(R(j:j,1)/a(j:j,j:j));

            

    y0(j:j,1)= x(j:j,1); 

    

   % disp (y0);    

   % disp (x);

end

 

if (abs(x(1:p,1)-x0(1:p,1)) < e(1:q,1)) % Error checking

    

    break;

    

end

 

disp (x);

disp(abs(x(1:p,1)-x0(1:p,1)));

    

x0=y0;

 

c=c+1;

 

end

 

x=x(1:p,1); % Returns solution

       

end

 

Program Outputs:

>> gauss_seidal([1 -1 4 0 2 9; 0 5 -2 7 8 4; 1 0 5 7 3 -2; 6 -1 2 3 0 8; -4 2 0 5 -5 3; 0 7 -1 5 4 -2], [19;2;13;-7;-9;2], [0; 0;0; 0; 0; 0],[0.05;0.05;0.05;0.05;0.05;0.05], 3)  % function calling

     6    -1     2     3     0     8    % rearranged matrix

     0     7    -1     5     4    -2

     1     0     5     7     3    -2

    -4     2     0     5    -5     3

     0     5    -2     7     8     4

     1    -1     4     0     2     9

   3.166666666666667   % first improved solutions

   0.285714285714286

   1.966666666666667

   1.019047619047619

  -1.703571428571429

  -0.593386243386244

   3.166666666666667   % error

   0.285714285714286

   1.966666666666667

   1.019047619047619

   1.703571428571429

   0.593386243386244

   2.840388007054674   % second improved solutions

   0.642705971277400

   1.390044091710759

  -0.732311665406903

  -0.241714380196523

  -0.586047738025251

   0.326278659611992   % error

   0.356991685563114

   0.576622574955908

   1.751359284454522

   1.461857048374905

   0.007338505360992

ans =                 % final solutions

   2.840388007054674

   0.642705971277400

   1.390044091710759

  -0.732311665406903

  -0.241714380196523

  -0.586047738025251

 

Percentage of error for the six solutions: 10.12%,  125%,  29%,  173%,  85%  and  1.1%. 

These errors may be the results of having a matrix, which is not diagonally dominant and the solution diverges as iteration increases.

Application of Gaussian Elimination to Solve System of Linear Algebraic Equations

Problem: In this example, we are going to solve the following system of linear algebraic equations by the widely-used Gaussian elimination method. Here, we are going to develop a MATLAB program that implements the Gaussian elimination to solve the following linear algebraic equations.

The following program implements Gaussian elimination method with partial pivoting and scaling to solve system of linear algebraic equations. The explanations of the codes are mentioned just right of each line.

MATLAB Program for Gauss Elimination Method

% Gaussian elimination with partial pivoting and scaling

 

function x = gausselimination(a,b)

 

% a - (nxn) matrix

% b - column vector of length n

 

format long;

 

m=size(a,1); % get number of rows in matrix a

 

n=length(b); % get length of b

 

if (m ~= n)

    

    error('a and b do not have the same number of rows')

    

end

 

a(:,n+1)=b;  % Forming (n,n+1) augmented matrix

 

for c=1:n

              

for r=c:m

     

% Scaling of the input matrix "a"

       

    Z(r,c) = a(r,c)/max(a(r,c:n));  % Scaling prior to pivoting 

 

    K(r:r,c:c)=Z(r,c); % Normalized coefficient parameters saved temporality 

                       % to another matrix "K"     

end

 

disp(K);

           

[~,f]=max(abs(K(1:r,c:c))); % Finding maximum absolute value from "K" matrix 

                            % for switching rows in matrix "a"      

disp(f);  

 

a([c,f],1:n+1)=a([f,c],1:n+1); % Switching between two rows 

                                                                                    

disp(a);

                                        

for i=c

% Making diagonal element of matrix "a" into 1.0

    

    a(i,i:n+1) = a(i,i:n+1)/a(i,i);   

 

for j=i+1:n

    

    % Making all elements below the diagonal element into zero

 

    a(j,i:n+1) = a(j,i:n+1) - a(j,i)*a(i,i:n+1);

    

end

 

end

 

disp(a);

 

end

 

% Process of back substitution

 

for j=n-1:-1:1

 

    a(j,n+1) = a(j,n+1) - a(j,j+1:n)*a(j+1:n,n+1);

 

end

    

% Returning solution

 

x=a(:,n+1);

 

end

Program Outputs:

ans =

 

  -1.761817043997860

   0.896228033874012

   4.051931404116157

  -1.617130802539541

   2.041913538501913

   0.151832487155935

Therefore, the solutions of the six linear algebraic equations are -1.76; 0.89; 4.05; -1.62; 2.04 and 0.15.

A PID Controller Design Method for DC Motor Speed Control

Control systems analysis and design focuses on three primary objectives:

•        producing the desired transient response
•        reducing steady state errors
•        achieving stability

Controller: Additional component or device that equalizes or compensates for the performance deficiency is called compensator or controller.

Plant: A system to be controlled.

Controller: Provides the excitation for the plant; Designed to control the overall system behavior.

There are several techniques available to the control systems engineer to design a suitable controller.

One of controller widely used is the proportional plus integral plus derivative (PID) controller, which has a transfer function:

Kp = Proportional gain

KI = Integral gain

Kd = Derivative gain

The signal (u) just past the controller is now equal to the proportional gain (Kp) times the magnitude of the error plus the integral gain (Ki) times the integral of the error plus the derivative gain (Kd) times the derivative of the error.

MATLAB Program:

Design requirements

Settling time less than 1 seconds

Overshoot less than 5%

Steady-state error less than 1%

Open-loop transfer function of the DC Motor:

Proportional Control:

j=3.2284e-6;

b=3.5077e-6;

k=0.0274;

r=4;

l=2.75e-6;

num=k;

kp =1.7;

den=[(j*l) ((j*r)+(l*b)) ((b*r)+k^2)  0];

sys=tf(num,den);

feedbk=feedback(kp*sys,1);

step(feedbk,0:.001:1)

Response Curve:

Proportional+Integral Control:

J=0.01;

b=0.1;

K=0.01;

R=1;

L=0.5;

num=K;

den=[(J*L) ((J*R)+(L*b)) ((b*R)+K^2)];

open_sys= tf(num,den);

subplot(2,1,1),step (open_sys,0:0.1:3);

step (open_sys,0:0.01:3);

title('Step Response for the Open Loop System');

kp = 100;

ki = 200;

kd = 0 ;

controller=tf([kd kp ki],[1 0]);

sys=feedback(controller*open_sys,1);

subplot(2,1,2),step (sys,0:0.01:3);

title('Closed loop Step:ki=100 kp=200');

Response Curve:

#Blog #Blogger #PID #PIDcontroller #DCmotor #ResponseCurve