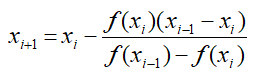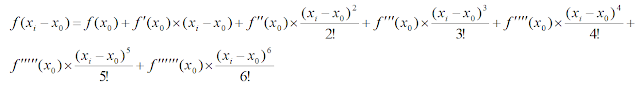Let's consider the following equation:
eˣ = 2x² + 1
We may write the above expression as,
f(x) = eˣ - 2x² - 1
To find the value of x or roots of the equation, we may apply the Secant method. In this method, the derivative may be approximated by a backward finite divided difference approach. So, the function may be expressed as,
This method is convenient when evaluating derivative for some function is difficult in Newton-Raphson method. Now, the above equation may be substituted in Newton-Raphson’s formula to get the following algorithm.
In contrast to Newton-Raphson method, two initial assumptions are made for the two unknowns’ xi-1 and xi.
For the proper initial guess for x, graphical method is applied to visualize the characteristics of the function. The MATLAB commands generate the plot of the function f(x). This function is plotted with respect to the values of x from -10 to +10. The following figure shows the function plot. From the plot, the function changes sign when x is between 2 to 3. So, the root lies in this interval. And, in the program developed for Secant method, two initial guesses for xi-1 and xi are 2 and 3 respectively.
However, more close observation reveals two roots, which are shown in the following figure. In this time, the range of x is decreased significantly for precise investigation between -2 to +2 as this interval seems unclear in the previous figure for the presence of any roots.
So, the above figure shows the existence of other two roots, which lie in between 0.1 to 1 and at the origin. The origin is obvious for this case, and there is no need for any further estimation by numerical methods. But, for the interval 0.1 to 1, the accurate and precise approximation is necessary. For this, the two initial guesses are set to 0.1 and 1 for xi-1 and xi accordingly.
The following Secant formula is implemented to approximate the two roots lie in the intervals 2 to 3 and 0.1 to 1. The results are shown after the program.
Secant Formula Implementation by a MATLAB Program
% Definition of a function "secant" to solve equation by Secant Method
function [x,ea] = secant(X,X0,etol)
format long;
% Input: X,X0, etol=Tolerance definition for error
% Output: x, ea=Calculated error in loop
% Iterative Calculations
while (1)
% Implementation of Secant Algorithm
solution = X-((exp(X)-(2*X^2)-1)*(X0-X))/((exp(X0)-(2*X0^2)-1)-(exp(X)-(2*X^2)-1));
solutionprevious=X;
X0=X;
X=solution;
if (solution-solutionprevious)~=0 % Approximate percent relative error
ea=abs((solution - solutionprevious)/solution)*100;
end
if ea<=etol,
break,
end
x = solution;
disp(x);
end
% Display of output parameters
disp(x);
disp(ea);
%disp(solution-(0.1*abs(ea)*solution));
end
Outputs:
>> secant (3, 2, 1e-5)
% Iterations
2.597424571529533
2.796706966294471
2.858723109017894
2.841817367110900
2.842657964680533
2.842673428005184
2.842673428005184
>> secant(1, 0.1, 1e-5)
% Iterations
0.308929151717719
0.570046187158243
1.157486960694727
0.682985699401547
0.723807551583747
0.742065590882227
0.740827136083267
0.740850398734311
0.740850398734311
So, the solutions for the equation are 2.842673428005184, 0.740850398734311 and 0.
#SecantMethod #RootsofEquations #Matlab #NumericalMethod #Blog #Blogger