Learning Mathematica, Lesson 3: Integration

Integration becomes very handy if you choose to use Wolfram Mathematica. You can evaluate definite and indefinite integrals using two ways.

1. You may use "Integrate[f, x]" command for the indefinite integrals, and "Integrate[f, {x, upper limit, lower limit}]" for the definite integrals.

2. Use int to enter ∫ and then use  to enter the lower limit, then 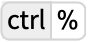 for the upper limit:

For example, if you would like to find out the following integral of a function using both approaches,

Now, let's look at another example, where you will find detailed Mathematica codes to determine the integral of the following:

Note that the following Mathematica program also implements a numerical integration scheme by using a built-in "NIntregate" command. Look carefully the systaxes used in the following codes to display the results, you may represent them in your own fashion.

Mathematica Codes:

(*Showing Exact Integration of First Problem*)

Print["Exact solution of \!\(\*SubsuperscriptBox[\(\[Integral]\), \

\(-1\), \(1\)]\)(2\!\(\*SuperscriptBox[\(x\), \(2\)]\)+3)\

\[DifferentialD]x"]

FullSimplify[\!\(

\*SubsuperscriptBox[\(\[Integral]\), \(-1\), \(1\)]\(\((2

\*SuperscriptBox[\(x\), \(2\)] + 3)\) \[DifferentialD]x\)\)]

(*Showing Numerical Integration of First Problem*)

Print["Numerical Integration by Approximation: \

\!\(\*SubsuperscriptBox[\(\[Integral]\), \(-1\), \

\(1\)]\)(2\!\(\*SuperscriptBox[\(x\), \(2\)]\)+3)\[DifferentialD]x"]

NIntegrate[(2 x^2 + 3), {x, -1, 1}]

Print["Numerical Integration by Gaussian Rule Order-1: \

\!\(\*SubsuperscriptBox[\(\[Integral]\), \(-1\), \

\(1\)]\)(2\!\(\*SuperscriptBox[\(x\), \(2\)]\)+3)\[DifferentialD]x"]

a = 2 x^2 + 3 /. x -> -Sqrt[1/(3)];

b = 2 x^2 + 3 /. x -> Sqrt[1/(3)];

c = N[a + b]

Program Output: