Encoders and Decoders
Optical encoders can be classified in two ways:
- Absolute Encoder
- Relative/Incremental Encoder
Encoders may have linear or rotary configurations. However, the rotary encoders are common in industry. In absolute encoder, a unique digital word corresponds to each rotational position of the shaft whereas in incremental encoder, by producing digital pulses while the shaft rotates measure the relative displacement of the shaft [1].
In this lab, Incremental encoder is studied and implemented. Incremental encoders are simple in construction and measurement as well.
Objectives
1. To develop a MATLAB program which decodes the input data streams “idatal8” given in the lab materials.
2. Then translating the written MATLAB code into a SIMULINK program.
3. Verification of the decoders by experiment comparing with the built-in decoders in the DC motor kit.
A MATLAB program is developed to decode the input data file “idatal8”. The steps and explanation of the commands are given as notes to the respective lines in the program. The entire program is given below which is based on the decoding logic given in table 1:
Table 1: Decoding of Optical Encoder Signal for Position Measurement [2]
Trigger
|
Other Channel
|
Motion Count
|
A rising (0 to
1)
|
B high (1)
|
-1
|
A rising (0 to
1)
|
B low (0)
|
+1
|
B rising (0 to
1)
|
A high (1)
|
+1
|
B rising (0 to
1)
|
A low (0)
|
-1
|
A falling (1 to
0)
|
B high (1)
|
+1
|
A falling (1 to
0)
|
B low (0)
|
-1
|
B falling (1 to
0)
|
A high (1)
|
-1
|
B falling (1 to
0)
|
A low (0)
|
+1
|
MATLAB Program for Decoding Input Data Streams
close all;
clear all;
format long;
idatal8 % Running the input data streams
t=1:179; % Total Sample
A=digdata(1,1:179); % Splitting the "digdata" into two workspaces
B=digdata(2,1:179);
j=1;
for i=1:178; % logic created for decoding input data
sum=0;
p=A(1,j);
q=B(1,j);
r=A(1,j+1);
s=B(1,j+1);
if r>p && q==0 % A rising & B low
count=1;
elseif p==1 && s>q % A high & B rising
count=1;
elseif r<p && q==1 % A falling & B high
count=1;
elseif p==0 && s<q % A low & B falling
count=1;
elseif p==0 && s>q % A low & B rising
count=-1;
elseif r>p && q==1 % A rising & B high
count=-1;
elseif p==1 && s<q % A high & B falling
count=-1;
elseif r<p && q==0 % A falling & B low
count=-1;
else
count=0;
end
sum=sum+count;
X(1,j)=sum; % Representing motion after decoding
j=j+1;
end
figure(1)
subplot (211),plot(t,A,'b'),grid
title('Sequence of Pulses vs Quadrature Signals')
ylabel ('Waveform from Channel A'),xlabel('Pulse Sequences')
subplot (212),plot(t,B,'r'),grid
title('Sequence of Pulses vs Quadrature Signals')
ylabel ('Waveform from Channel B'),xlabel('Pulse Sequences')
figure(2) % Decoded Motion
t1=1:178;
plot(t1,X,'b'),grid
title('Forward & Reverse Motion')
ylabel ('Waveform'),xlabel('Motion Counts')
Following figure 1 shows the waveform from channel A and B plotted separately obtained from the data file ‘idatal8’. Figure 2 represents the motion count after decoding the input data streams which eventually dictate the forward and reverse direction by the program algorithm. This figure also highlights the fast and slow sequences of the counts.
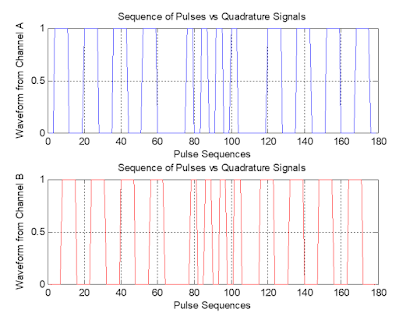
Figure 1: Showing the signals from channel A and B from input data streams ‘idatal8’.
Objective 2
An incremental or quadrature encoder provides two bit signal. Each signal comes from each of the receivers (channel A and B). These two input streams are offset by ¼ of one of the light or dark bands. For an incremental encoder, the will be four discrete positions for each pulse. These positions are (0,0), (1,0), (1,1) and (0,1). Depending on these 4 distinct positions, the direction of rotation of the motor may be determined by the following table.
Table 2: Direction of Motion Assessment
Forward Motion
|
Channel A
|
|
Channel B
|
||
Backward
Motion
|
Channel A
|
|
Channel B
|
A SIMULINK model is created to understanding the position and velocity counting mechanisms of the encoder which is connected to the “DC Motor Kit”. Following figure 3 shows the simple model for the experiment. In the experiment, attempts are taken to measure the resolution of
the physical encoder. For this, first the total number of discrete positions is counted for one revolution. For one revolution, there are 7820 distinct points and number of bands or slots on the disk is 1955 (7820/4). For one revolution, the encoder count decreases from 0 to -3950 and then increases to -80 and based on this information the 7820 discrete points are estimated. This calculation
might vary, but would provide some insights into position measurement. So, the resolution of the experimental encoder is 0.04º (360/7820) approximately. For each positive or negative counts, there will be a change of position of the motor around 0.04º that the encoder measures.
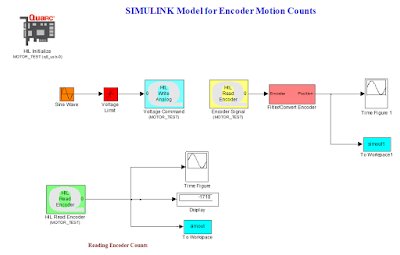
Figure 3: A SIMULINK model for
understanding encoding and decoding.
Objective 3
In this part, the algorithm developed earlier in Objective-1 will be verified. For this, the encoder total counts for a single rotation is gathered and stored in the workspace. A truncated data table is provided below to show the trend of the encoder counts.
Table 3: Encoder Reading Pattern from the Experiment
|
-1467
-1465
-1463
-1461
-1459
-1457
-1455
-1453
-1451
|
Data Truncated
|
-1701
-1703
-1705
-1707
-1709
-1711
-1713
-1715
-1716
-1718
|
To verify the MATLAB program, the similar program with some modifications is done which decodes the above data streams. The program for the physical encoder decoding is given below:
MATLAB Program for Decoding Physical Encoder Counts
close all;
clear all;
format long;
inputdatastreams % Running data file
t=(1:2707)';
A=counts;
j=1;
for i=1:2707;
sum=0;
p=A(j,1);
q=A(j+1,1);
if q>p % Decoding logics
count=-1;
elseif q<p
count=1;
else
count=0;
end
sum=sum+count;
X(j,1)=sum; % Stores positive/negative counts
j=j+1;
end
figure(1)
plot(t,X,'b'),grid
title('Forward & Reverse Motion')
ylabel ('Waveform'),xlabel('Motion Counts')
Figure 4 shows the decoded signals from the encoder. From the figure, it is observed that the data streams have forward motion, reverse motion, fast and slow rate with the increase of time.
Figure 4: Showing the decoded signal from encoder data streams.
References
[1] David G. Alciatore, Michael B. Histand, Introduction to Mechatronics and Measurement Systems-fourth edition, The McGraw-Hill Companies, Inc., 2012.
[2] Dr. Jeff Pieper, ENME 560 (Mechatronics Design Laboratory), Lab-05 Manual, 2006.
#Encoder #Decoder #IncrementalEncoder #DataStream #SIMULINK #Blog #Blogger



No comments:
Post a Comment